【Unity】ComputeShaderでランタイムにSDFマップを生成するエクスペリメント
【Unity】ComputeShaderでランタイムにSDFマップを生成するエクスペリメント:
この記事はカヤックUnityアドベントカレンダー2018の23日目の記事です。
「面白法人カヤック」をUnityでのダイナミックフォントで普通に描画するとこうなります。

SDFマップのフォントアトラスを生成したら、ベベルや影など、リッチなエフェクトがリアルタイムで描画できるようになります。

しかし、そのSDFマップの生成処理は結構時間がかかります。なので漢字とカタカナのキャラクターセット「面」、「白」、「法」、「人」、「カ」、「ヤ」、「ッ」、「ク」が入っているSDFマップを事前に生成しないと作れないですね。
今回のエクスペリメントではそのマップをランタイムで生成できるようにして、こんなエフェクトが作れるようになります。

どうやってでしょうか?まずは SDF マップについて軽く紹介します。
そして去年 Unity 2017 に統合されたTextMeshProプラグインがこのSDFマップを利用します。おかげでリッチなフォントのエフェクトがリアルタイムで表現できます。しかし、その SDF マップを生成するのに結構時間がかかり、エディターで事前に生成する必要があります。アルファベットを使っているゲームには特に問題がないですが、漢字を使っている日本または中国のゲームでは問題になるかもしれません。漢字を利用するゲームではダイナミックフォントをよく使っているため、事前にSDFマップを生成することができません。そのために今回は初めてCompute Shaderを触りながら、CPUで処理していたSDFマップの生成を、GPUで処理してランタイムで生成できるようにしようと思います。
このCPUの実装は基本的に3つのステップに別れています:
最初のステップはSobelフィルターです。各ピクセルのアウトプットは3x3の隣接するピクセルで計算され、部分的に処理されるので自然に並列化できます。
これをすべてのピクセルに対して行うことにより、各ピクセルが1x1の局所的SDFマップになります。この手法を反復すると、これらの小さな1x1SDFマップは、その近隣と重複する3x3のSDFマップになります。これを反復で実行することによって、完全なSDFマップを作成することができます。
反復処理毎に全てのスレッドの処理が完了しないと次の反復処理は実行できません。そのためにグローバルなスレッド同期が必要ですが、そのためのHLSLのキーワード
上記のテーブルによりますと、距離制限が最大に設定されていても、GPUの方がまだCPUより26~51倍早いと示しています。NVIDIAやAMDのちゃんとしたGPUじゃなくても、こんなスピードアップができるのは正直びっくりしました。
両方の結果を比較すると、GPUで生成されたSDFマップは、形状の内側のグラデーションがより短いとわかります。これによって、内側に表現したいベベルなどのエフェクトが若干浅くなりそうですね。対策案としては、距離計算のチューニングか、距離ベクターからalphaテクスチャーへ書き出しのポストプロセスでなんとか調整できそうな気がします。
明日の記事は荻原さんによる「CINEMA 4D+Unityでクリスマスイルミネーションを作る」です。
はじめに
こんにちは、ソーシャルゲーム事業部 ゲーム技研所属のアファトです。この記事はカヤックUnityアドベントカレンダー2018の23日目の記事です。
「面白法人カヤック」をUnityでのダイナミックフォントで普通に描画するとこうなります。

SDFマップのフォントアトラスを生成したら、ベベルや影など、リッチなエフェクトがリアルタイムで描画できるようになります。

しかし、そのSDFマップの生成処理は結構時間がかかります。なので漢字とカタカナのキャラクターセット「面」、「白」、「法」、「人」、「カ」、「ヤ」、「ッ」、「ク」が入っているSDFマップを事前に生成しないと作れないですね。
今回のエクスペリメントではそのマップをランタイムで生成できるようにして、こんなエフェクトが作れるようになります。

どうやってでしょうか?まずは SDF マップについて軽く紹介します。
Signed Distance Field (SDF) とは
Signed Distance Field は Signed Distance Function という関数から生成されます。その関数は簡単に言いますと、ある座標から輪郭までの最短の距離の関数です。Signedというのはシェイプの外か中かによって符号が違うことを指します。具体的に言うと、シェイプの中にある座標は距離がポジティブで、外の場合は距離がネガティブになります。そしてフィールド内の全座標からこの関数を評価すると Signed Distance Field が作れます。今回は2次元の表示のため、この記事で書いてあるSDFは2次元のSDFのことになります。そして去年 Unity 2017 に統合されたTextMeshProプラグインがこのSDFマップを利用します。おかげでリッチなフォントのエフェクトがリアルタイムで表現できます。しかし、その SDF マップを生成するのに結構時間がかかり、エディターで事前に生成する必要があります。アルファベットを使っているゲームには特に問題がないですが、漢字を使っている日本または中国のゲームでは問題になるかもしれません。漢字を利用するゲームではダイナミックフォントをよく使っているため、事前にSDFマップを生成することができません。そのために今回は初めてCompute Shaderを触りながら、CPUで処理していたSDFマップの生成を、GPUで処理してランタイムで生成できるようにしようと思います。
CPUでSDFマップを生成する処理の実装
参考とするCPUベースSDFマップ生成処理は Anti-aliased Euclidean distance transform のペーパーに基づいた Unity AssetStoreにある Catlike Coding SDF Texture Generator のツールです。 Valve社のペーパー で使われている入力データと違って、このツールの入力データはアンチエイリアスのかかった白黒テクスチャーなのです。そのため高解像度バイナリテクスチャーを用意する必要がありません。このCPUの実装は基本的に3つのステップに別れています:
- Sobel フィルター: 輪郭とエッジの方向(ノーマル)
- アンチエイリアスエッジとの距離の計算( このペーパー のメインテクニック)
- SSED-8 (eight-points signed sequential Euclidean distance transform) での距離ベクターの伝播
Sobel フィルター
class Pixel
{
public float alpha; // Inputテクスチャーのアルファ
public float distance;
public Vector2 gradient;
public int dX, dY;
}
void ComputeEdgeGradients (Pixel[,] pixels)
{
float sqrt2 = Mathf.Sqrt(2f);
for(int y = 1; y < height - 1; y++)
{
for(int x = 1; x < width - 1; x++)
{
Pixel p = pixels[x, y];
if(p.alpha > 0f && p.alpha < 1f)
{
// 周りのalphaで方向を計算する
float g =
- pixels[x - 1, y - 1].alpha
- pixels[x - 1, y + 1].alpha
+ pixels[x + 1, y - 1].alpha
+ pixels[x + 1, y + 1].alpha;
p.gradient.x = g + (pixels[x + 1, y].alpha - pixels[x - 1, y].alpha) * sqrt2;
p.gradient.y = g + (pixels[x, y + 1].alpha - pixels[x, y - 1].alpha) * sqrt2;
p.gradient.Normalize();
}
}
}
}
アンチエイリアスエッジへの距離の計算
float ApproximateEdgeDelta (float gx, float gy, float a)
{
// (gx, gy) エッジへの方向
if(gx == 0f || gy == 0f){
return 0.5f - a;
}
// (gx, gy) をノーマライズ
float length = Mathf.Sqrt(gx * gx + gy * gy);
gx = gx / length;
gy = gy / length;
// シンメトリーなので、最初の象限だけで十分
// gx >= 0, gy >= 0, gx >= gy
gx = Mathf.Abs(gx);
gy = Mathf.Abs(gy);
if(gx < gy){
float temp = gx;
gx = gy;
gy = temp;
}
// デルタの計算
float a1 = 0.5f * gy / gx;
if(a < a1){
// 0 <= a < a1
return 0.5f * (gx + gy) - Mathf.Sqrt(2f * gx * gy * a);
}
if(a < (1f - a1)){
// a1 <= a <= 1 - a1
return (0.5f - a) * gx;
}
// 1-a1 < a <= 1
return -0.5f * (gx + gy) + Mathf.Sqrt(2f * gx * gy * (1f - a));
}
void GenerateInitialEdgeDistances (Pixel[,] pixel)
{
int x, y;
Pixel p;
// 距離の初期化
for(y = 0; y < height; y++)
{
for(x = 0; x < width; x++)
{
p = pixels[x, y];
p.dX = 0;
p.dY = 0;
if(p.alpha <= 0f)
{
// シェイプの外
p.distance = 1000000f;
}
else if (p.alpha < 1f)
{
// シェイプのエッジ
p.distance = ApproximateEdgeDelta(p.gradient.x, p.gradient.y, p.alpha);
}
else
{
// シェイプの中
p.distance = 0f;
}
}
}
}
SSED-8での距離ベクターの伝播
void PropagateEdgeDistance(Pixel[,] pixels)
// 8SSED (eight-points signed sequential Euclidean distance transform)を実行する
// 上
for(y = 1; y < height; y++){
// |P.
// |XX
p = pixels[0, y];
if(p.distance > 0f){
UpdateDistance(p, 0, y, 0, -1);
UpdateDistance(p, 0, y, 1, -1);
}
// -->
// XP.
// XXX
for(x = 1; x < width - 1; x++){
p = pixels[x, y];
if(p.distance > 0f){
UpdateDistance(p, x, y, -1, 0);
UpdateDistance(p, x, y, -1, -1);
UpdateDistance(p, x, y, 0, -1);
UpdateDistance(p, x, y, 1, -1);
}
}
// XP|
// XX|
p = pixels[width - 1, y];
if(p.distance > 0f){
UpdateDistance(p, width - 1, y, -1, 0);
UpdateDistance(p, width - 1, y, -1, -1);
UpdateDistance(p, width - 1, y, 0, -1);
}
// <--
// .PX
for(x = width - 2; x >= 0; x--){
p = pixels[x, y];
if(p.distance > 0f){
UpdateDistance(p, x, y, 1, 0);
}
}
}
// 下
for(y = height - 2; y >= 0; y--){
// XX|
// .P|
p = pixels[width - 1, y];
if(p.distance > 0f){
UpdateDistance(p, width - 1, y, 0, 1);
UpdateDistance(p, width - 1, y, -1, 1);
}
// <--
// XXX
// .PX
for(x = width - 2; x > 0; x--){
p = pixels[x, y];
if(p.distance > 0f){
UpdateDistance(p, x, y, 1, 0);
UpdateDistance(p, x, y, 1, 1);
UpdateDistance(p, x, y, 0, 1);
UpdateDistance(p, x, y, -1, 1);
}
}
// |XX
// |PX
p = pixels[0, y];
if(p.distance > 0f){
UpdateDistance(p, 0, y, 1, 0);
UpdateDistance(p, 0, y, 1, 1);
UpdateDistance(p, 0, y, 0, 1);
}
// -->
// XP.
for(x = 1; x < width; x++){
p = pixels[x, y];
if(p.distance > 0f){
UpdateDistance(p, x, y, -1, 0);
}
}
}
}
GPU実装アイデア
GPUで計算するために、各ステップを効率的に並列化しないといけません。GPUに適したメモリアクセスパターンなどを考慮する必要がありますが、今回はCompute Shaderへの踏み台としてそこまで深く最適化しません。最初のステップはSobelフィルターです。各ピクセルのアウトプットは3x3の隣接するピクセルで計算され、部分的に処理されるので自然に並列化できます。
#define TWO_SQRT 1.41421356237
groupshared float gs_input[BLOCK_SIZE_X][BLOCK_SIZE_Y];
inline float2 CalcGradientSobel(float diag1, float diag2, float dh, float dv)
{
float gx = diag1 + diag2 + dh * TWO_SQRT;
float gy = diag1 - diag2 + dv * TWO_SQRT;
return float2(gx, -gy);
}
inline float2 GetGradient(int2 id)
{
float diag1 =
- gs_input[id.x-1][id.y+1]
+ gs_input[id.x+1][id.y-1];
float diag2 =
- gs_input[id.x-1][id.y-1]
+ gs_input[id.x+1][id.y+1];
float right = gs_input[id.x+1][id.y];
float left = gs_input[id.x-1][id.y];
float down = gs_input[id.x][id.y-1];
float up = gs_input[id.x][id.y+1];
return CalcGradientSobel(diag1, diag2, right - left, down - up);
}
次のステップはアンチエイリアスエッジとの距離の計算です。各ピクセルを処理するために必要なデータがそれ自体に含まれているので、そのまま並列化することができます。いくつか分岐が入ってますが、とりあえずスルーします。inline float ApproximateDistance (float2 grad, float a)
{
grad = normalize(grad);
grad = abs(grad);
float gx = grad.x;
float gy = grad.y;
grad.xy = float2(max(gx, gy), min(gx, gy));
gx = grad.x;
gy = grad.y;
float a1 = 0.5 * gy / gx;
if (a < a1)
{
return 0.5 * (gx + gy) - sqrt(2 * gx * gy * a);
}
if (a < (1 - a1))
{
return (0.5 - a) * gx;
}
return -0.5 * (gx + gy) + sqrt(2 * gx * gy * (1 - a));
}
そしてカーネルは次のようになりますRWTexture2D<float4> InputTex;
RWTexture2D<float3> GradResult;
#define GROUP_COL 16
#define GROUP_ROW 4
[numthreads(GROUP_COL, GROUP_ROW, 1)]
void GradientPass (uint3 id : SV_DispatchThreadID, uint3 tid : SV_ThreadID, uint3 gid : SV_GroupThreadId)
{
LoadInput(); // デバイスメモリから groupshared gs_input にロードする
float2 grad = GetGradient(tid);
bool isEdge = // エッジかどうかは
+ step(abs(alpha - 0.5), 0.499) // 0 < alpha < 1 か
+ step(2.5, length(grad)) > 0; // はっきりしたエッジ (adhoc)
float2 distance = isEdge //エッジじゃなかったら無限の距離にアサインする
? normalize(grad) * ApproximateDistance(grad, alpha)
: infinite;
GradResult[id.xy] = float3(
distance,
sign(alpha - 0.5) // シェイプの中か外の情報
);
}
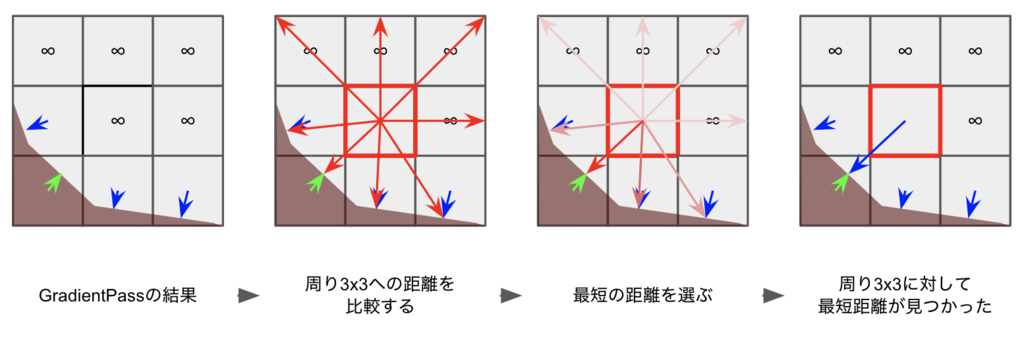
問題は最後のステップです。SSED-8アルゴリズムはピクセルを順番に処理しないと正しい結果が得られないので、直接並列化することが出来ません。なのでGPUに適した違うアプローチが必要です。シンプルなアプローチとして局所的にSDFマップを生成するようにします。局所的というのは、各ピクセルが周りの3x3のピクセルに対して、輪郭までの最短の距離ベクターを持つことです。そうするとSobelフィルターみたいに各ピクセルを平行で実行できるようになります。
これをすべてのピクセルに対して行うことにより、各ピクセルが1x1の局所的SDFマップになります。この手法を反復すると、これらの小さな1x1SDFマップは、その近隣と重複する3x3のSDFマップになります。これを反復で実行することによって、完全なSDFマップを作成することができます。
反復処理毎に全てのスレッドの処理が完了しないと次の反復処理は実行できません。そのためにグローバルなスレッド同期が必要ですが、そのためのHLSLのキーワード
globallycoherent はなんだか効果がなかったみたいです。とりあえず一回の反復はカーネルを一回実行するという解決にします。そうすると、NxNのテクスチャーのSDFマップを生成するために、カーネルをN/2回実行します。幸いなことに、フォントレンダリングのための典型的なSDFマップは、一定のピクセル数に制限された距離情報しか必要としません(大体4~10ピクセル)。これにより、必要とされるカーネル呼び出しの数がその値に制限されます。したがって、オーバーヘッドは、並列化によるパフォーマンスの向上と比べて小さいです。パフォーマンス
テスト用のマシンはIntel Iris Graphics 550 GPU(1.5GBのメモリ)と3.3GHzのIntel Core i7 CPUを搭載した13インチのMacBook Pro 2017を使用しました。この反復手法では、SDFマップを生成するのに必要な時間は距離制限に大きく依存します。その一方でCPUでのSDF生成処理に必要な時間は、距離制限に対して不変(常に最大限距離)であるため、最大限の距離制限をテストする必要があります。そのため、いくつかSDFマップの距離制限をテストします: 10px、20px、40px、および最大限の距離(テクスチャーの対角線のピクセル数)。| 解像度 | CPU SDF | GPU SDF 距離制限10px | GPU SDF 距離制限20px | GPU SDF 距離制限40px | GPU SDF 最大限の距離 |
|---|---|---|---|---|---|
| 256x256 | 1347 ms | 8 ms | 10 ms | 15 ms | 26 ms |
| 512x512 | 5356 ms | 9 ms | 13 ms | 18 ms | 129 ms |
| 1024x1024 | 20732 ms | 13 ms | 19 ms | 33 ms | 790 ms |
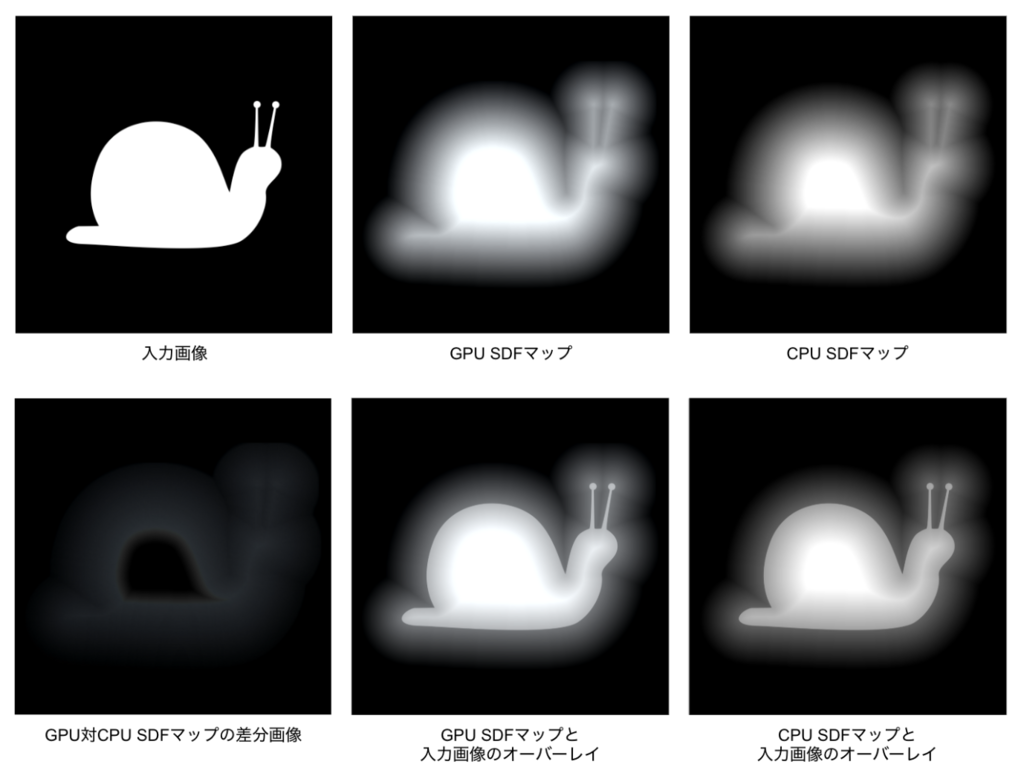
CPUとGPUで生成されたSDFマップの比較

両方の結果を比較すると、GPUで生成されたSDFマップは、形状の内側のグラデーションがより短いとわかります。これによって、内側に表現したいベベルなどのエフェクトが若干浅くなりそうですね。対策案としては、距離計算のチューニングか、距離ベクターからalphaテクスチャーへ書き出しのポストプロセスでなんとか調整できそうな気がします。
まとめ
これはGPU上のプロセスを最適化せずに単純に並列化しようとするCompute Shaderの試みなので、大きな改善の余地があるはずです。それでも CPUのプロセスに比べるとパフォーマンスが大幅に向上しました。これで、ランタイム時にSDFマップを生成することができ、ダイナミックフォントを使用してもTextMeshProと同様にフォントレンダリングに豊富なエフェクトを表現することが可能になります。明日の記事は荻原さんによる「CINEMA 4D+Unityでクリスマスイルミネーションを作る」です。
| オリジナルのエンクロージャ: |

コメント
コメントを投稿