色：ヘキサコードから眼球まで – Part 3.
色：ヘキサコードから眼球まで – Part 3.:
注釈：
スペクトル軌跡のrg色度
波長（um）
色の点が付いた黒の曲線は全てのスペクトル純色の色度を示しています。曲線はスペクトル軌跡と呼ばれ、星印は等色実験で使用される可変出力試験灯の波長をマークしたものです。
前述した色度の三角形をこの表に重ねると、次のようになります。
注釈：
スペクトル軌跡のrg色度
波長（um）
スペクトル軌跡内の領域は、人間が見ることができる全ての色度を表しています。ただし格子模様の領域については、人は認識できますが、435nm、546nm、700nmの光を正の方向にどれだけ加算しても再現はできません。また、この図から、純粋なシアンを含む435nmから546nmの間のスペクトル色は再現できないことが分かります。
格子模様のない右側の三角形は、正の方向の加算で再現できる色度です。色空間のこの再現できる領域を色域と呼びます。
最終的にヘキサコードに戻る前に、もう1つ触れておくべき色空間があるので、次はそちらを見ていきましょう。
XYZ色空間の目的の1つは、人間の視認可能な色の全てを正の値で表せるようにすることであり、従って、全ての色度が両軸上の[0、1]の範囲に収まるようにすることでした。これを達成するために、RGB空間の一次変換が注意深く行われました。
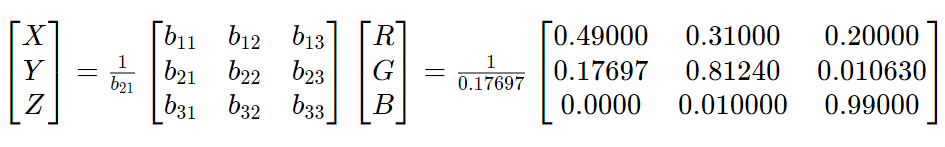
XYZ空間においてrg色度の代わりとなるのはxy色度です。この座標系は、色度図ではより一般的に使われています。
注釈：
xy色度図
通常、色域はxy色度図に配置された三角形によって表されます。例として、ここで再びCIE RGBの色域を、今回はxy空間で示してみましょう
注釈：
CIE RGBの色域
色域と色度について理解できたら、次はやっとデジタルディスプレイがどのように意図された色を表示するかについての検討に入ります。
等色実験で使われる試験灯とは異なり、サブピクセルの色は1つではありません。各サブピクセルが固有の分光分布を有しており、この分光分布は機器によって異なります。
f.luxometerによるMacBook Airのサブピクセルのスペクトルデータ
MacBook ProのColorSyncユーティリティを使うと、自分のディスプレイのxy空間の色域を決定することができます。
注釈：
MacBook ProのLCDの色域
ここで目に付くのが、色域の角がスペクトル軌跡に沿っていないということです。サブピクセルは純粋な単色光ではないので、これは不思議なことではありません。この色域は、MacBook ProのLCDディスプレイが忠実に再現できる色度の全範囲を示しています。
ディスプレイの色域は製品により様々ですが、現代のディスプレイであれば特定の色域はカバーできようにした方がいいでしょう。その色域とはsRGBです。
その規格では、赤、緑、および青の原色の色度が指定されています。
これらをプロットすると、MacBookのLCDディスプレイに類似した（ただし、わずかに小さい）色域になります。
注釈：
MacBook ProのLCDの色域
sRGBの色域
一部の箇所では、MacBook ProのLCDディスプレイの色域からsRGBの（正式な）色域がはみ出ています。つまりこの部分については、LCDは忠実に色を再現できません。これに対応するため、MacBookでは変更を加えたsRGBの色域を使っているようです。
注釈：
正式なsRGBの色域
MacBook ProのLCDの色域
MacBook ProのsRGBの色域
sRGBはデフォルトの色空間として広く利用されています。また、ブラウザの標準的な色空間（CSS標準で指定）でもあります。このブログの記事の図で使われているのは全てsRGB空間内の色です。逆に言うと、sRGB空間外の色であれば、正確に再現されないということになります。
それでは最後に、ウェブ上で色がどのように指定されるかについて見ていきましょう。
0x9B/0xFF = 0.61
0x51/0xFF = 0.32
0xE0/0xFF = 0.88
その結果、
これらの値をディスプレイ機器に送信してサブピクセルの輝度を設定する前に、もう1つやることがあります。それはガンマ補正です。
人間の視覚は、高エネルギー光線における小さな変化より、低エネルギー光線における小さな変化に対しての方が、ずっと敏感です。そのため、256の値を低エネルギーの値により多くを割り当てることが望ましいと言えます。
どのようにするかを確認するために、グレースケールの値を3ビットだけで符号化すると考えてください。取り得る値は8通りになります。
グレーの値をエネルギーの線形関数としてプロットすると、以下のようになります。
注釈：
線形エネルギー
3ビットで符号化した値をYとします。符号化した値を均等に配置すると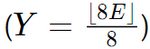
、以下のようになります。
注釈：
線形エネルギー
Y=0とY=1の間の知覚的な違いは、Y=6とY=7の間の知覚的な違いよりはるかに大きいことが分かります。
それでは代わりに、べき関数を使うとどうなるかを見てみましょう。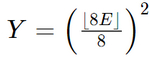
を試してみます。
注釈：
線形エネルギー
知覚的な差がかなり近づいてきました。隣接する値の差は他の隣接する値の差と同程度となっています。
エネルギー値を離散値にマッピングする、このような過程はガンマエンコーディングと呼ばれています。この逆の操作（離散値をエネルギー値に変換）はガンマデコーディングと言います。
通常、ガンマ補正は方程式Vout=AVinγとなります。指数がギリシャ文字の”ガンマ”なので、ガンマ補正という名前が付いています。
sRGBはエンコーディングやデコーディングのルールに使われる考え方は似ていますが、より複雑です。
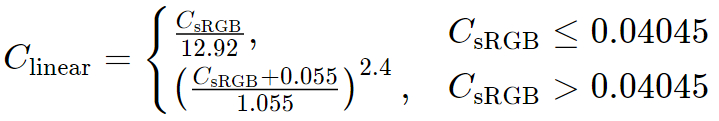
sRGB値を線形値に対してプロットすると以下のようになります。
注釈：
線形エネルギー
線形RGB
sRGB
線形知覚明度
これがヘキサコードから眼球への伝達過程を理解するために必要な最後の情報でした。それでは順を追って見ていきましょう。
これは、sRGB空間において座標（0.61, 0.32, 0.88）となります。次にsRGBの要素を線形値に変換します。
そうすると、線形RGB空間において座標（0.33, 0.08, 0.10）となります。これらの値はスクリーン上におけるサブピクセルの輝度設定に使用されます。
サブピクセルの分光分布が組み合わさり、1つのピクセルに対する1つの分光分布となります。
注釈：
波長（nm）
このピクセルからの電磁放射線は角膜を通って網膜に到達し、3種類の錐体細胞を刺激します。
注釈：
目に届く放射線
錐体細胞の感度
錐体細胞の励起
網膜錐体の励起
これらを全てまとめると、本投稿の冒頭の図のようになります。
注釈：
波長（nm）
網膜錐体の励起
sRGB値は、サブピクセルの明度に変換される前に、機器の明るさ設定によって弱められます。例えば、ディスプレイの明るさ50％の時の
理想的なスクリーンでは、明るさの設定に関わらず、黒いピクセル（0, 0, 0）は光を発しません。しかし携帯電話やノートパソコンでは、ほとんどの場合、それぞれのサブピクセルが白色光のフィルターとなるLCDが採用されています。LCDの詳しい働きについては、こちらの動画をご覧ください。
このフィルターは不完全なので、明るさが増すと、バックライトが漏れて黒いピクセルが光を放ちます。有機EL画面（iPhone XやPixel 2など）はバックライトを使用しないため、画面の明るさに影響されず黒の一貫性が維持されます。
本稿では、これらについて説明しません。もうすでに、かなり長い記事になっていますからね。私の友人は「世の中は見た目よりも奥が深いものばかりだ。しかし、それを分かっていても、色は更に予想を超えて奥が深い」と言っています。
以下は特に役立つショートリストです。
* 測色のビギナーズガイド
* CIE 1931 色空間
* HSLとHSV
* ガンマ補正
* リアルタイム レンダリング 第3版 p210-217
また、本稿では多くのデータ表を使ってグラフを描きました。
こちらの記事を気に入っていただけましたら、twitterで私をフォローしてください。または、私の他の投稿をご覧になったり、私と一緒にFigmaで働いたりしましょう。
色域とスペクトル軌跡
等色関数rˉ(λ)、gˉ(λ)、およびbˉ(λ)を取り、それらを使ってスペクトル色のrg色度をプロットすると、その結果は以下のようになります。注釈：
スペクトル軌跡のrg色度
波長（um）
色の点が付いた黒の曲線は全てのスペクトル純色の色度を示しています。曲線はスペクトル軌跡と呼ばれ、星印は等色実験で使用される可変出力試験灯の波長をマークしたものです。
前述した色度の三角形をこの表に重ねると、次のようになります。
注釈：
スペクトル軌跡のrg色度
波長（um）
スペクトル軌跡内の領域は、人間が見ることができる全ての色度を表しています。ただし格子模様の領域については、人は認識できますが、435nm、546nm、700nmの光を正の方向にどれだけ加算しても再現はできません。また、この図から、純粋なシアンを含む435nmから546nmの間のスペクトル色は再現できないことが分かります。
格子模様のない右側の三角形は、正の方向の加算で再現できる色度です。色空間のこの再現できる領域を色域と呼びます。
最終的にヘキサコードに戻る前に、もう1つ触れておくべき色空間があるので、次はそちらを見ていきましょう。
CIE XYZ色空間
1931年、国際照明委員会が開催され、2つの色空間を作りました。そのうちの1つはすでに説明したRGB色空間です。この色空間はライトとギルドの等色実験の結果に基づいて作成されました。そして2つ目はXYZ色空間です。XYZ色空間の目的の1つは、人間の視認可能な色の全てを正の値で表せるようにすることであり、従って、全ての色度が両軸上の[0、1]の範囲に収まるようにすることでした。これを達成するために、RGB空間の一次変換が注意深く行われました。
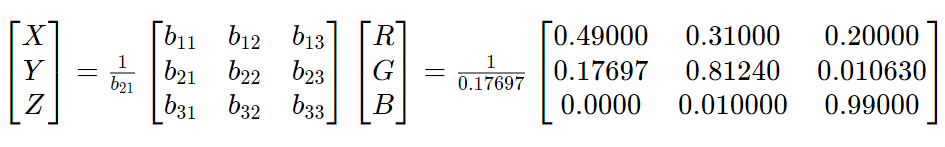
XYZ空間においてrg色度の代わりとなるのはxy色度です。この座標系は、色度図ではより一般的に使われています。
注釈：
xy色度図
通常、色域はxy色度図に配置された三角形によって表されます。例として、ここで再びCIE RGBの色域を、今回はxy空間で示してみましょう
注釈：
CIE RGBの色域
色域と色度について理解できたら、次はやっとデジタルディスプレイがどのように意図された色を表示するかについての検討に入ります。
画面のサブピクセル
ディスプレイの製造元にかかわらず、強力なルーペで画面を見れば、ピクセルグリッドが見えるはずです。各ピクセルは、それぞれ赤、緑、青を放射する3種類のサブピクセルで構成されています。図にすると、以下のような感じです。等色実験で使われる試験灯とは異なり、サブピクセルの色は1つではありません。各サブピクセルが固有の分光分布を有しており、この分光分布は機器によって異なります。
f.luxometerによるMacBook Airのサブピクセルのスペクトルデータ
MacBook ProのColorSyncユーティリティを使うと、自分のディスプレイのxy空間の色域を決定することができます。
注釈：
MacBook ProのLCDの色域
ここで目に付くのが、色域の角がスペクトル軌跡に沿っていないということです。サブピクセルは純粋な単色光ではないので、これは不思議なことではありません。この色域は、MacBook ProのLCDディスプレイが忠実に再現できる色度の全範囲を示しています。
ディスプレイの色域は製品により様々ですが、現代のディスプレイであれば特定の色域はカバーできようにした方がいいでしょう。その色域とはsRGBです。
sRGB
sRGB（”standard RGB”）は、色データをメディア間で忠実に転送することを目的に、HPとMicrosoftが1996年に作成した色空間です。その規格では、赤、緑、および青の原色の色度が指定されています。
| 色度 | 赤 | 緑 | 青 |
|---|---|---|---|
| x | 0.6400 | 0.3000 | 0.1500 |
| y | 0.3300 | 0.6000 | 0.0600 |
| Y | 0.2126 | 0.751 | 0.0722 |
注釈：
MacBook ProのLCDの色域
sRGBの色域
一部の箇所では、MacBook ProのLCDディスプレイの色域からsRGBの（正式な）色域がはみ出ています。つまりこの部分については、LCDは忠実に色を再現できません。これに対応するため、MacBookでは変更を加えたsRGBの色域を使っているようです。
注釈：
正式なsRGBの色域
MacBook ProのLCDの色域
MacBook ProのsRGBの色域
sRGBはデフォルトの色空間として広く利用されています。また、ブラウザの標準的な色空間（CSS標準で指定）でもあります。このブログの記事の図で使われているのは全てsRGB空間内の色です。逆に言うと、sRGB空間外の色であれば、正確に再現されないということになります。
それでは最後に、ウェブ上で色がどのように指定されるかについて見ていきましょう。
sRGBヘキサコード
#9B51E0はsRGB空間で色を指定します。その色を、対応する（R、G、B）座標に変換する場合、3つの要素のそれぞれを0xFF（255）で割らなければなりません。この場合、以下のようになります。0x9B/0xFF = 0.61
0x51/0xFF = 0.32
0xE0/0xFF = 0.88
その結果、
#9B51E0に対応する座標は（0.61,0.32,0.88）です。これらの値をディスプレイ機器に送信してサブピクセルの輝度を設定する前に、もう1つやることがあります。それはガンマ補正です。
ガンマ補正
256個の値を取り得るRGB空間の各座標において、隣接する値の色は可能な限り識別できることが望ましいと言えます。例えば、#030000と#040000は、#F40000と#F50000が異なるのと同じように区別したいということです。人間の視覚は、高エネルギー光線における小さな変化より、低エネルギー光線における小さな変化に対しての方が、ずっと敏感です。そのため、256の値を低エネルギーの値により多くを割り当てることが望ましいと言えます。
どのようにするかを確認するために、グレースケールの値を3ビットだけで符号化すると考えてください。取り得る値は8通りになります。
グレーの値をエネルギーの線形関数としてプロットすると、以下のようになります。
注釈：
線形エネルギー
3ビットで符号化した値をYとします。符号化した値を均等に配置すると
、以下のようになります。注釈：
線形エネルギー
Y=0とY=1の間の知覚的な違いは、Y=6とY=7の間の知覚的な違いよりはるかに大きいことが分かります。
それでは代わりに、べき関数を使うとどうなるかを見てみましょう。
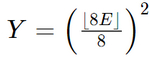を試してみます。注釈：
線形エネルギー
知覚的な差がかなり近づいてきました。隣接する値の差は他の隣接する値の差と同程度となっています。
エネルギー値を離散値にマッピングする、このような過程はガンマエンコーディングと呼ばれています。この逆の操作（離散値をエネルギー値に変換）はガンマデコーディングと言います。
通常、ガンマ補正は方程式Vout=AVinγとなります。指数がギリシャ文字の”ガンマ”なので、ガンマ補正という名前が付いています。
sRGBはエンコーディングやデコーディングのルールに使われる考え方は似ていますが、より複雑です。
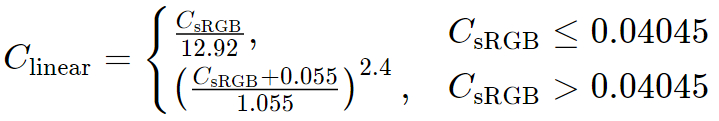
sRGB値を線形値に対してプロットすると以下のようになります。
注釈：
線形エネルギー
線形RGB
sRGB
線形知覚明度
これがヘキサコードから眼球への伝達過程を理解するために必要な最後の情報でした。それでは順を追って見ていきましょう。
ヘキサコードから眼球へ
まず#9B51E0をR、G、Bの要素に分けます。これらの要素の範囲は[0、1]です。これは、sRGB空間において座標（0.61, 0.32, 0.88）となります。次にsRGBの要素を線形値に変換します。
そうすると、線形RGB空間において座標（0.33, 0.08, 0.10）となります。これらの値はスクリーン上におけるサブピクセルの輝度設定に使用されます。
サブピクセルの分光分布が組み合わさり、1つのピクセルに対する1つの分光分布となります。
注釈：
波長（nm）
このピクセルからの電磁放射線は角膜を通って網膜に到達し、3種類の錐体細胞を刺激します。
注釈：
目に届く放射線
錐体細胞の感度
錐体細胞の励起
網膜錐体の励起
これらを全てまとめると、本投稿の冒頭の図のようになります。
注釈：
波長（nm）
網膜錐体の励起
輝度設定について
sRGB値は、サブピクセルの明度に変換される前に、機器の明るさ設定によって弱められます。例えば、ディスプレイの明るさ50％の時の
0xFF0000は、同じディスプレイの明るさ100％の時の0x7F0000に相当します。理想的なスクリーンでは、明るさの設定に関わらず、黒いピクセル（0, 0, 0）は光を発しません。しかし携帯電話やノートパソコンでは、ほとんどの場合、それぞれのサブピクセルが白色光のフィルターとなるLCDが採用されています。LCDの詳しい働きについては、こちらの動画をご覧ください。
このフィルターは不完全なので、明るさが増すと、バックライトが漏れて黒いピクセルが光を放ちます。有機EL画面（iPhone XやPixel 2など）はバックライトを使用しないため、画面の明るさに影響されず黒の一貫性が維持されます。
書き切れなかったこと
本稿では、色の再現や認知に関する内容について、かなりの量の情報を意図的に省きました。例えば、反対色説や色の恒常性の影響に関して、錐体細胞が励起する情報と脳の働きについて説明していません。加法混色の原色と減法混色の原色の比較も行いませんでした。色盲にも触れていません。光束、光度、輝度、照度、光束発散度の違いについても説明を省いています。ICCプロファイルやf.luxなどのプログラムが色覚に与える影響についても述べませんでした。本稿では、これらについて説明しません。もうすでに、かなり長い記事になっていますからね。私の友人は「世の中は見た目よりも奥が深いものばかりだ。しかし、それを分かっていても、色は更に予想を超えて奥が深い」と言っています。
参考文献
今お読みいただいた本稿は、執筆に多くの時間を要しました。なぜなら、書いている間に納得のいく説明のできていない部分が次から次へと出てきたからです。以下は特に役立つショートリストです。
* 測色のビギナーズガイド
* CIE 1931 色空間
* HSLとHSV
* ガンマ補正
* リアルタイム レンダリング 第3版 p210-217
また、本稿では多くのデータ表を使ってグラフを描きました。
- University College London Color & Vision Research Laboratoryのデータベース（XYZ等色関数、錐体分光感度）
- fluxometer.com（RGB 液晶画面サブピクセルスペクトル）
- CIE 15: Technical Report: Colorimetry, 3rd edition（RGB等色関数）
こちらの記事を気に入っていただけましたら、twitterで私をフォローしてください。または、私の他の投稿をご覧になったり、私と一緒にFigmaで働いたりしましょう。
コメント
コメントを投稿